General Description
X-ray Diffraction (XRD) is a high-tech, non-destructive technique for analyzing a wide range of materials, including fluids, metals, minerals, polymers, catalysts, plastic, pharmaceuticals, thin film coatings, ceramics, solar cells, and semi conductors. Throughout industry and research institutions, XRD has become an indispensable method for materials investigation, characterization and quality control. Example areas of application include qualitative and quantitative phase analysis, crystallography, structure and relaxation determination, texture and residual stress investigations, controlled sample environment, micro-diffraction, nano-materials, lab- and process automation, and high-throughput polymorph screening.
About 95% of all solid materials can be described as crystalline. When X-rays interact with a crystalline substance (Phase), one gets a diffraction pattern.
In 1919 A.W.Hull gave a paper titled, “A New Method of Chemical Analysis”. Here he pointed out that “….every crystalline substance gives a pattern; the same substance always gives the same pattern; and in a mixture of substances each produces its pattern independently of the others. “
The X-ray diffraction pattern of a pure substance is, therefore, like a fingerprint of the substance. The powder diffraction method is thus ideally suited for characterization and identification of polycrystalline phases.
Today about 50,000 inorganic and 25,000 organic single components, crystalline phases, and diffraction patterns have been collected and stored on magnetic or optical media as standards. The main use of powder diffraction is to identify components in a sample by a search/match procedure. Furthermore, the areas under the peak are related to the amount of each phase present in the sample.
THEORETICAL CONSIDERATIONS
In order to better convey an understanding of the fundamental principles and buzz words of X-ray diffraction instruments, let us quickly look at the theory behind these systems. (The theoretical considerations are rather primitive; hopefully they are not too insulting).
Solid matter can be described as:
Amorphous:
The atoms are arranged in a random way similar to the disorder we find in a liquid.
Glasses are amorphous materials.
Crystalline:
The atoms are arranged in a regular pattern, and there is as smallest volume element that by repetition in three dimensions describes the crystal. E.g. we can describe a brick wall by the shape and orientation of a single brick. This smallest volume element is called a unit cell. The dimensions of the unit cell are described by three axes:
When a crystal is bombarded with X-rays of a fixed wavelength (similar to spacing of the atomic-scale crystal lattice planes) and at certain incident angles, intense reflected X-rays are produced when the wavelengths of the scattered X-rays interfere constructively. In order for the waves to interfere constructively, the differences in the travel path must be equal to integer multiples of the wavelength. When this constructive interference occurs, a diffracted beam of X-rays will leave the crystal at an angle equal to that of the incident beam.
To illustrate this feature, consider a crystal with crystal lattice planar distances d (right). Where the travel path length difference between the ray paths ABC and A'B'C' is an integer multiple of the wavelength, constructive interference will occur for a combination of that specific wavelength, crystal lattice planar spacing and angle of incidence θ. Each rational plane of atoms in a crystal will undergo refraction at a single, unique angle (for X-rays of a fixed wavelength).
Bragg's Law reflection. The diffracted X-rays exhibit constructive interference when the distance between paths ABC and A'B'C' differs by an integer number of wavelengths (λ).
The general relationship between the wavelength of the incident X-rays, angle of incidence and spacing between the crystal lattice planes of atoms is known as Bragg's Law, expressed as:
n λ = 2d sin θ
where n (an integer) is the "order" of reflection, λ is the wavelength of the incident X-rays, d is the interplanar spacing of the crystal and θ is the angle of incidence.
The X-ray Powder Method
In practice, this would be a time consuming operation to reorient the crystal, measure the angle q, and determine the d-spacing for all atomic planes. A faster way is to use a method called the powder method. In this method, a mineral is ground up to a fine powder. In the powder, are thousands of grains that have random orientations. With random orientations we might expect most of the different atomic planes to lie parallel to the surface in some of the grains. Thus, by scanning through an angle q of incident X-ray beams form 0 to 90o, we would expect to find all angles where diffraction has occurred, and each of these angles would be associated with a different atomic spacing.
The instrument used to do this is an x-ray powder diffractometer. It consists of an X-ray tube capable of producing a beam of monochromatic X-rays that can be rotated to produce angles from 0 to 90o. A powdered mineral sample is placed on a sample stage so that it can be irradiated by the X-ray tube. To detect the diffracted X-rays, an electronic detector is placed on the other side of the sample from the X-ray tube, and it too is allowed to rotate to produce angles from 0 to 90o.
Reference of Figure: http://www.xos.com/techniques/xrd/parallel-beam-geometryfor-powder-x-ray-diffraction/
The instrument used to rotate both the X-ray tube and the detector is called a goniometer. The goniometer keeps track of the angle q, and sends this information to a computer, while the detector records the rate of X-rays coming out the other side of the sample (in units of counts/sec) and sends this information to the computer.
After a scan of the sample the X-ray intensity can be plotted against the angle q (usually reported as 2θ because of the way older diffractometers were made) to produce a chart, like the one shown here. The angle 2θ for each diffraction peak can then be converted to d-spacing, using the Bragg equation.
One can then work out the crystal structure and associate each of the diffraction peaks with a different atomic plane in terms of the Miller Index for that plane (hkl).
A group known as the Joint Committee on Powder Diffraction Standards (JCPDS) has collected data such as this on thousands of crystalline substances. This data can be obtained as the JCPDS Powder Diffraction File. Since every compound with the same crystal structure will produce an identical powder diffraction pattern, the pattern serves as kind of a "fingerprint" for the substance, and thus comparing an unknown mineral to those in the Powder Diffraction file enables easy identification of the unknown. We will see how this is done in our laboratory demonstration.
Types of XRD Analysis
Phase Analysis
- Airborne particulate analysis and estimation including quartz, cristobolite, vanadium and zinc Oxide analysis as per OSHA standards
- Detailed soil and clay mineral analysis
- Crystalline/Amorphous ratio-Percent Crystallinity in polymers and ceramic materials
- Structural characterization and analysis of catalysts and chemicals
- Analysis of corrosion products
- Corrosion and Materials failure analysis
Quantitative Analysis
- Accurate phase quantification by Rietveld Method
- External and Internal standard methods.
Rietveld Analysis
- Accurate quantitative analysis by whole pattern fitting least squares technique
- Accurate lattice parameter determination
- Line broadening analysis (Crystallite size determination Microstrain determination)
Retained Austenite Determination
- The Rietveld method will be used to quantify the amounts of Austenite in stainless steel.
Thin Film Analysis
- Low angle glancing incidence technique for extremely thin films
- Thickness determination
- Determination of preferred orientation
Case studies
Using X-Ray diffraction BRUKER D8 couple with EVA software analysis
Qualitative analysis
Qualitative analysis usually involves the identification of a phase or phases in a specimen by comparison with “standard” patterns (PDF-Data Base), and relative estimation of proportions of different phases in multiphase specimens by comparing peak intensities attributed to the identified phases.
- Go ‘START’ menu and ‘click’ or open ‘EVA’ software
- EVA window will be on display. Import spectra file through ‘Import’ menu in ‘File’ tab. Then select ‘Scan File’.or You can import file by ‘Import’ tab at toolbar. ‘Import Scan Files’ window will be displayed.
- Select your scan file (*.RAW)
Note: A "scan" is the diffractogram, i.e. the measured data set, which is the result of intensity collection with a powder diffractometer; it is stored in a file with the extension .RAW. Note that EVA imports the data, i.e. it works with a copy of the data, the original RAW file is never changed, so you can always come back to the beginning.
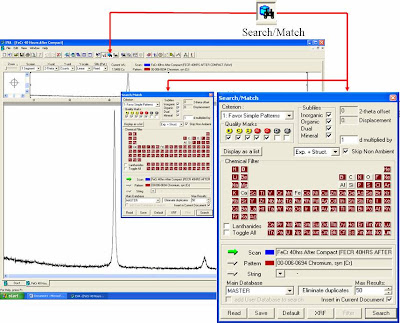
- A ‘diifractograph’ of your scanned data will appear on the ‘doc’ window. As example, this is the spectra of pure Fe powder. Let’s make a qualitative study first to identify whether this scanned material is a pure Fe or not.
- We need to match the pattern of difrractograph with reference pattern.Go to ‘Toolbox’ tab or ‘search/menu’ in ‘View’ tab.
- oWe need to match the pattern of difrractograph with reference pattern (ICDD-PDF-2 Data Base). Go to ‘search/match’ tab or push ‘F3’ or ‘search/menu’ in ‘View’ tab.
- You need to set ‘chemical filter’ and ‘quality mark’ according to your preference.
The result was clearly identify as Chromium-Iron with PDF No: 03-065-7775
Quantitative analysis
Quantitative analysis of diffraction data usually refers to the determination of amounts of different phases in multi-phase samples. Quantitative analysis may also be thought of in terms of the determination of particular characteristics of single phases including precise determination of crystal structure or crystallite size and shape.
Measuring crystallite size using Williamson-Hall plott
The first description of size broadening was given by Scherrer in 1918, although the first rigorous theory of line broadening was formulated in 1944. Williamson-Hall size-strain analysis was developed in 1953 as a method to separate size and strain effects by their angular dependence.
B.1 Size broadening
Sherrer (1918) first observed that small crystallite size could give rise to line broadening. He drived a well known equation for relating the crystallite size to the broadening, which is called the scherrer formula(Shecerrer, 1918; Langford & Wilson, 1978).
D = Volume weighted crystallite size
K = Scherrer constant, some what arbitrary value that falls in the range 0.87-1.0
λ = The wav e lenght of the radiation
B = The integral breadth or FWHM of reflection peaks (in radians) located at 2θ
B.2 Strain broadening
Stokes and Wilson (1944), they included the lattice strain as another source of broadening, than broadening that arises from small crystallite size (Langford & Wilson, 1978).
εstrain = Weighted average strain
B = The integral breadth or FWHM of reflection peaks (in radians) located at 2θ
B.3 Williamson-Hall analysis
The diffraction pattern gradually broadens with milling duration and the broadening is due to simultaneous size and strain effects. High-energy ball-milling introduces considerable strain in the lattice and its contribution to line broadening is not negligible. Williamson and Hall (Williamson, 1953) developed a method to separate these two effects and that is known as the Williamson–Hall plot. The Williamson-Hall equation is given by:
Bcorrected cosθ =  +
+  (B.3)
(B.3)
where Bcorrected is full width at half maximum (FWHMcorrected) of the XRD peak, K is the Scherrer constant, D is the crystallite size, λ is the X-ray wavelength, ε is the lattice strain and θ is the Bragg angle.
B.3 Correcting for instrumental effects
Before estimating the crystallite size and lattice strain, it is necessary to correct the instrumental effect. To decouple these contributions, it is necessary to collect a diffraction pattern from the line broadening of a standard material such as Si (Silicon) and LaB6 (lanthanum hexaboride) (Zak et al., 2011; He, 2009; Mittemeijer & Welzel, 2008), to determine the instrumental broadening. The instrument-corrected broadening (B) corresponding to the diffraction peak of specimen was estimated using the relation Gaussian profiles (Saryanto et al., 2010; Raman &Gupta, 2009; He, 2009; Venkateswarlu & Rameshbabu, 2010):
Bcorrected = B2obs – B2instrument (B.4)
where B is the instrumental corrected full width at half maximum (FWHM) in radians, Bobserved is full width at half maximum (FWHM) from diffraction peaks of specimens and Binst is standard peaks of the standard reference materials (LaB6: NIST SRM 660a), as shown in Figure B.1.











No comments:
Post a Comment